Simulation algorithms for atomic DEVS
Given an atomic DEVS model, simulation algorithms are methods to generate the model's legal behaviors which are trajectories not to reach to illegal states. (see Behavior of DEVS). [Zeigler84] originally introduced the algorithms that handle time variables related to lifespan ![t_s \in [0,\infty]](/2012-wikipedia_en_all_nopic_01_2012/I/645b86302c4e4314f43d086938a2d48d.png) and elapsed time
and elapsed time 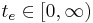 by introducing two other time variables, last event time,
by introducing two other time variables, last event time, 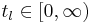 , and next event time
, and next event time ![t_n\in [0,\infty]](/2012-wikipedia_en_all_nopic_01_2012/I/54455b4692504a6b5a5754bb3f186163.png) with the following relations:
with the following relations:
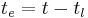
and
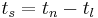
where 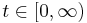 denotes the current time. And the remaining time,
denotes the current time. And the remaining time,
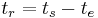
is equivalently computed as
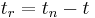
, apparently ![t_r \in [0,\infty]](/2012-wikipedia_en_all_nopic_01_2012/I/533eb3d11640c0feccc0f83da207dd6e.png) .
.
Since the behavior of a given atomic DEVS model can be defined in two different views depending on the total state and the external transition function (refer to Behavior of DEVS), the simulation algorithms are also introduced in two different views as below.
Contents |
Common parts
Regardless of two different views of total states, algorithms for initialization and internal transition cases are commonly defined as below.
DEVS-simulator
variables:
parent // parent coordinator
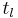 // time of last event
// time of last event
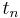 // time of next event
// time of next event
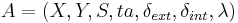 // the associated Atomic DEVS model
when receive init-message(Time
// the associated Atomic DEVS model
when receive init-message(Time  )
)
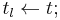
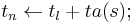 when receive star-message(Time
when receive star-message(Time  )
if
)
if 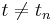 then
error: bad synchronization;
then
error: bad synchronization;
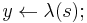 send y-message(
send y-message(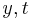 ) to parent;
) to parent;
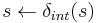
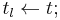
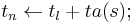
View 1: total states = states * elapsed times
As addressed in Behavior of Atomic DEVS, when DEVS receives an input event, right calling  , the last event time,
, the last event time, is set by the current time,
is set by the current time, , thus the elapsed time
, thus the elapsed time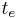 becomes zero because
becomes zero because 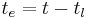 .
.
when receive x-message(, Time
) if
and
== false then error: bad synchronization;
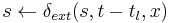
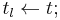
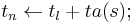
View 2: total states = states * lifespans * elapsed times
Notice that as addressed in Behavior of Atomic DEVS, depending on the value of  return by
return by 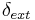 , last event time,
, last event time,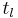 , and next event time,
, and next event time,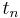 ,consequently, elapsed time,
,consequently, elapsed time, 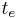 , and lifespan
, and lifespan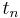 , are updated (if
, are updated (if 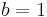 ) or preserved (if
) or preserved (if 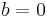 ).
).
when receive x-message(, Time
) if
and
== false then error: bad synchronization;
if
then
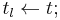
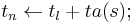
See also
References
- [Zeigler84] Bernard Zeigler (1984). Multifacetted Modeling and Discrete Event Simulation. Academic Press, London; Orlando. ISBN 978-0127784502.
- [ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0127784557.